The given data set is 21,31,26,24,28,26.
Arranging the data set in the ascending order,
21,24,26,26,28,31.
The data set contains 6 numbers,
The median can be determined by taking the average of 3rd and 4th term of the data set,
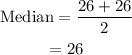
Thus, the required median is 26.
The range can be determined by taking the difference between the highest and the lowest value of the data set,

Thus, the range of the data set is 10.
The interquartile range of the data set can be determined by taking the difference of quartile 1 and quartile 3.
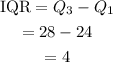
Thus, the required interquartile range is 4.