Question

A student pushes a heavy box that is originally stationary across the floor with a force 112 N. What is the coefficient of static friction between the classroom floor and the 140 N box?

Answer 1

Given data:

* The force applied on the heavy box is,

`F_a=112\text{ N}`

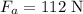
* The weight of the heavy box is,

`w=140\text{ N}`

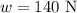
Solution:

The frictional force acting on the box is,

`\begin{gathered} F_r=\mu* w \\ \mu\text{ is the coefficient of friction,} \end{gathered}`

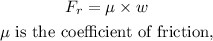
The frictional force acting on the heavy box is equal to the applied force as the heavy box is not moving under the action of applied force.

Thus,

`\begin{gathered} F_r=F_a \\ \mu* w=112 \\ \mu*140=112 \\ \mu=(112)/(140) \end{gathered}`

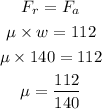
By simplifying,

`\mu=0.8\text{ }`

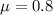
Thus, the coefficient of friction between the floor and the box is 0.8.