Given:
The mass of player 1 is m1 = 82 kg
The initial velocity of player 1 is
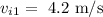
towards left.
The mass of player is m2 = 76 kg
The initial velocity of player 2 is
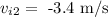
in opposite direction.
Required:
The final velocity after the collision assuming they stick together.
The loss of kinetic energy after collision.
Step-by-step explanation:
According to the conservation of momentum, the final velocity will be

The loss in kinetic energy will be
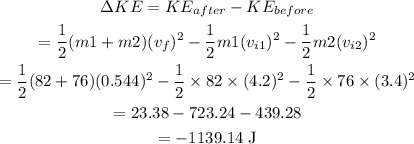
Final Answer:
The final velocity after the collision assuming they stick together is 0.544 m/s.
The loss of kinetic energy after the collision is 1139.14 J.