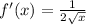Question

Find from first principles the derivative of f(x)= root of X with respect to x

Answer 1

To find:

The derivative of function f(x) using the first principle.

`f(x)=√(x)`

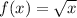
Solution:

By the first principle, the derivative of the function f(x) is given by:

`f^(\prime)(x)=\lim_(h\to0)(f(x+h)-f(x))/(h)`

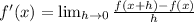
So, the derivative of the given function can be obtained as follows:

`\begin{gathered} f^(\prime)(x)=\lim_(h\to0)(√(x+h)-√(x))/(h) \\ =\lim_(h\to0)(√(x+h)-√(x))/(h)*(√(x+h)+√(x))/(√(x+h)+√(x)) \\ =\lim_(h\to0)(x+h-x)/(h(√(x+h)+√(x))) \\ =\lim_(h\to0)(h)/(h(√(x+h)+√(x))) \\ =\lim_(h\to0)(1)/((√(x+h)+√(x))) \\ =(1)/(√(x+0)+√(x)) \\ =(1)/(2√(x)) \end{gathered}`

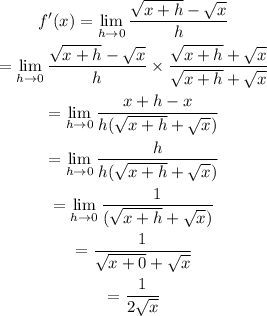
Thus, the derivative of the given function is:

`f^(\prime)(x)=(1)/(2√(x))`