Question

How to write a rule for the nth term of the geometric seq

Answer 1

`a_n=7(4)^(n-1)`

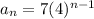
Explanations:

The nth term of a geometric sequence is expressed as:

`a_n=ar^(n-1)`

were:

• a is the first term

,

• r is the common ratio

,

• n is the number of terms

If the 2nd term a₂ = 28, then;

`\begin{gathered} 28=ar^(2-1) \\ ar=28 \end{gathered}`

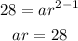
If the 5th term a₅ = 1792, then;

`\begin{gathered} 1792=ar^(5-1) \\ ar^4=1792 \end{gathered}`

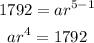
Take the ratio of both equations to have:

`\begin{gathered} (ar^4)/(ar)=(1792)/(28) \\ r^3=64 \\ r=\sqrt[3]{64} \\ r=4 \end{gathered}`

Substitute r = 4 into any of the equations to have:

`\begin{gathered} ar=28 \\ 4a=28 \\ a=(28)/(4) \\ a=7 \end{gathered}`

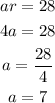
Determine the rule for the nth term of the geometric sequence. Recall that;

`\begin{gathered} a_n=ar^(n-1) \\ a_n=7(4)^(n-1) \end{gathered}`

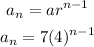
This gives the nth term of the geometric sequence