To answer this question, we can graph both lines equations using the intercepts of both lines. The intercepts are the x- and the y-intercepts for both lines.
The x-intercept is the point where the line passes through the x-axis. At this point, y = 0. Likewise, the y-intercept is the point where the line passes through the y-axis. At this point, x = 0.
Therefore, we can proceed as follows:
1. Graphing the line y = 2x - 9
First, we can find the x-intercept. For this, y = 0.
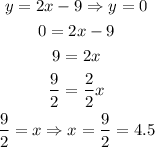
Therefore, the x-intercept is (4.5, 0).
The y-intercept is:
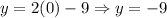
Therefore, the y-intercept is (0, -9).
With these two points (4.5, 0) and (0, -9) we can graph the line y = 2x - 9.
2. Graphing the line y = -(1/2)x +1
We can proceed similarly here.
Finding the x-intercept:

Therefore, the x-intercept is (2, 0).
Finding the y-intercept:
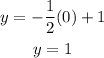
Then the y-intercept is (0, 1).
Now we can graph this line by using the points (2, 0) and (0, 1).
Graphing both lines
To graph the line y = 2x - 9, we have the following coordinates (4.5, 0) and (0, -9) ---> Red line.
To graph the line y = -(1/2)x + 1, we have the coordinates (2, 0) and (0, 1) ---> Blue line.
We graph both lines, and the point where the two lines intersect will be the solution of the system:
We can see that the point where the two lines intersect is the point (4, -1). Therefore, the solution for this system is (4, -1).
We can check this if we substitute the solution into the original equations as follows:
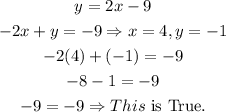
And
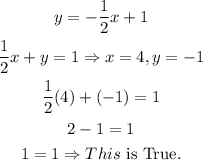
In summary, we found the solution of the system:
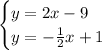
Using the intercepts of the lines, graphing the lines, and the point where the two lines intersect is the solution for the system. In this case, the solution is (4, -1) or x = 4, and y = -1.