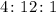Firstly, let x represent Alex's age, y represent George's age and z represent Carl's age.
from the question;
Alex is 12 years older than George, So;

Carl is three times older than Alex, So;
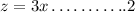
The sum of their ages is 68, So;

Now we have three equations and three unknowns, so it is solvable.
Let us substitute equation 2 into equation 3; that is replace z with 3x in equation 3.
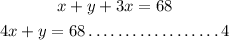
Next, let us substitute equation 1 into equation 4. that is replace x with y+12 in equation 4.
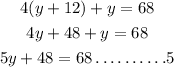
we can now solve for the value of y from equation 5.
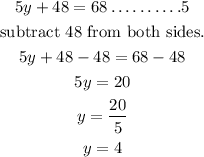
let us now replace y with 4 in equation 1 to get the value of x. since y = 4;
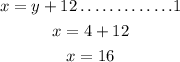
then, since x =16 let us replace x with 16 in equation 2 to get z.
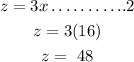
so we have;
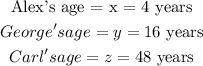
We now need to find the ratio of George, Carl and Alex's age.
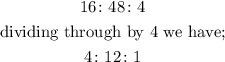
So the ratio of their ages are;