Question

According to a survey, 62% of Americans go on vacation each year. Two Americans are chosen from a group of 100 Americans what is the probability that one or both of the people chosen does not go on vacation each year?

Answer 1

61.56%

Step-by-step explanation:

Let the first American = A

• P(A goes) = 0.62

,

• P(A does not) = 0.38

Let the second American = B

• P(B goes) = 0.62

,

• P(B does not) = 0.38

The probability that one or both of the people chosen does not go on vacation each year

=P(A goes and B does not) or P(A does not and B does) or P(both do not)

`\begin{gathered} =P(AB^(\prime))+P(A^(\prime)B)+P(A^(\prime)B^(\prime)) \\ =(0.62*0.38)+(0.38*0.62)+(0.38*0.38) \\ =0.2356+0.2356+0.1444 \\ =0.6156 \end{gathered}`

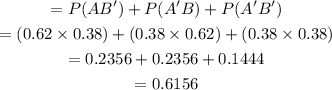
Therefore, the probability that one or both of the people chosen does not go on vacation each year is 61.56%.