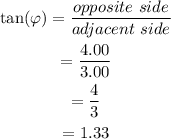Question

In the figure below, find each of the following.A right triangle has a vertical side labeled "3.00", a horizontal side labeled "4.00" that goes rightwards from the bottom of the vertical side, and a hypotenuse labeled "5.00" that goes down and right from the top of the vertical side to the right of the horizontal side. The top left interior angle of the triangle is an acute angle and the bottom right interior angle is an acute angle .(a) the length of the side opposite (b) the length of the side adjacent to (c) cos()(d) sin()(e) tan()

Answer 1

Given

To find:

a) The length of the side opposite

(b) The length of the side adjacent to

(c) cos()

(d) sin()

(e) tan()

Step-by-step explanation:

It is given that,

That implies,

(a) The length of the side opposite is 3.00.

(b) The length of the side adjacent to is 3.00.

(c) cos()

`\begin{gathered} \cos(\theta)=\frac{adjacen\text{t }side}{hypotenuse} \\ =(4.00)/(5.00) \\ =(4)/(5) \\ =0.8 \end{gathered}`

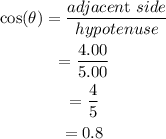
(d) sin()

`\begin{gathered} \sin(\varphi)=\frac{opposite\text{ }side}{hypotenuse} \\ =(4.00)/(5.00) \\ =(4)/(5) \\ =0.8 \end{gathered}`

(e) tan()

`\begin{gathered} \tan(\varphi)=\frac{opposite\text{ }side}{adjacent\text{ }side} \\ =(4.00)/(3.00) \\ =(4)/(3) \\ =1.33 \end{gathered}`