The equation of a circle with center (h, k) and radius r is given by the following expression:

In this case, the center of the circle is located at (6, -4), and its radius equals 6, then by replacing 6 for h, -4 for k and 6 for r, we get:
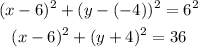
Then, the last option is the correct answer: (x - 6)^2 + (y + 4)^2 = 36