Question

A 0.0215 m diameter coin rolls up a 20.0 degree inclined plane. The coin starts with an initial angular speed of 55.2 rad/ s and rolls in a straight line without slipping. How much vertical height does it gain before it stops rolling?

Answer 1

The coin will reach a vertical height of 0.027 meters before it stops rolling.

Step-by-step explanation:

Let suppose that coin-ground system is a conservative system and begins at a height of zero. Since the coin is experimenting a general plane motion, which is a combination of translation and rotation. By Principle of Energy Conservation we have the following model:

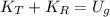`K_(T)+K_(R) = U_(g)` (1)

Where:

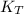`K_(T)` - Translational kinetic energy at the bottom of the incline, in joules.

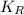`K_(R)` - Rotational kinetic energy at the bottom of the incline, in joules.

`U_(g)` - Gravitational potential energy at the top of the incline, in joules.

By definitions of Kinetic and Gravitational Potential Energy we expand (1):

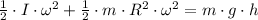`(1)/(2)\cdot I \cdot \omega ^(2) + (1)/(2)\cdot m\cdot R^(2)\cdot \omega^(2) = m\cdot g\cdot h` (2)

Where:

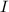`I` - Momentum of inertia of the coin, in kilogram-square meters.

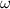`\omega` - Angular speed, in radians per second.

`R` - Radius of the coin, in meters.

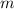`m` - Mass, in kilograms.

`g` - Gravitational acceleration, in meters per square second.

`h` - Height reached by the coin, in meters.

The momentum of inertia of the coin is calculated by:

`I = (1)/(2)\cdot m\cdot r^(2)` (3)

Then, we expand and simplify (2):

`(3)/(4)\cdot R^(2)\cdot \omega^(2) = g\cdot h`

`h = (3\cdot R^(2)\cdot \omega^(2))/(4\cdot g)`

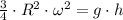
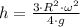
If we know that
`R = 0.0108\,m`,
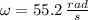`\omega = 55.2\,(rad)/(s)` and
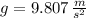`g = 9.807\,(m)/(s^(2))`, then the height reached by the coin is:

`h = 0.027\,m`

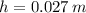
The coin will reach a vertical height of 0.027 meters before it stops rolling.