Question

Determine if the following equation is linear if the equation is linear converted to standard form AX+by=c

Answer 1

Given the equation:

`(-10+y^2)-y^2=-7x+10`

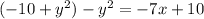
To determine if the equation is a linear equation, the first step is to simplify it. To do so, erase the parentheses and simplify the like terms:

`\begin{gathered} (-10+y^2)-y^2=7x+10 \\ -10+y^2-y^2=7x+10 \\ -10+0y^2=7x+10 \\ -10+0y=7x+10 \end{gathered}`

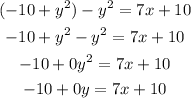
The terms "+y²" and "-y²" canceled each other, this is why the variable y is multiplied by zero. Then the only variable left is "x", which suggests that the equation represents a vertical line.

To write this equation in standard form, you have to pass the x-term to the left side of the equation and the constant to the right side of it:

The line written in standard form is 7x+0y=20.

Vertical lines are considered to be linear equations.