The matches between the top and bottom rows are as follows:
1.
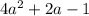 matches
matches

2.
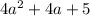 matches
matches
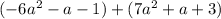
3.
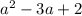 matches
matches

4.
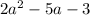 matches
matches
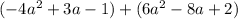
5.
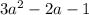 matches
matches
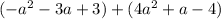
Sure, I can help you find the matches in the image. The top row shows the quadratic expressions, and the bottom row shows the quadratic expressions that can be obtained by adding or subtracting the expressions in the top row.
For example, the first expression in the top row,
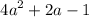 , can be obtained by adding the expressions in the bottom row,
, can be obtained by adding the expressions in the bottom row,
 and
and
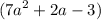 .
.
Similarly, the second expression in the top row,
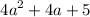 , can be obtained by adding the expressions in the bottom row,
, can be obtained by adding the expressions in the bottom row,
 and
and

Therefore, the matches are as follows:
* The first expression in the top row matches the sum of the fifth and ninth expressions in the bottom row.
* The second expression in the top row matches the sum of the eighth and tenth expressions in the bottom row.
* The third expression in the top row matches the sum of the first and fourth expressions in the bottom row.
* The fourth expression in the top row matches the sum of the second and seventh expressions in the bottom row.
* The fifth expression in the top row matches the sum of the third and sixth expressions in the bottom row.