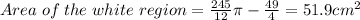Question

find the area of the white region ...blue region has a 150 degree triangle with 7cm side and the circle has a radius of 7

Answer 1

First, let's find the area circular sector:

`A=(r^2\theta)/(2)`

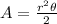
Where:

r = radius = 7cm

θ = angle (in radians) = 5/6 π

so:

`\begin{gathered} A=(7^2((5)/(6)\pi))/(2) \\ A=(245)/(12)\pi \end{gathered}`

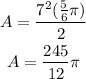
Now, let's find the area of the triangle, that triangle is an isosceles triangle, so, we can use the following formula in order to find its area:

`\begin{gathered} At=(1)/(2)s^2\cdot\sin (\theta) \\ \end{gathered}`

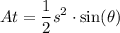
where:

s = one of the equal sides = 7

θ = angle = 150

so:

`\begin{gathered} At=(1)/(2)(7^2)\sin (150) \\ At=(49)/(4) \end{gathered}`

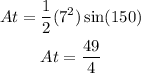
Therefore, the area of the white region will be, the area of the circular sector minus the area of the isosceles triangle, so:

`Area_{\text{ }}of_{\text{ }}the_{\text{ }}white_{\text{ }}region=(245)/(12)\pi-(49)/(4)=51.9cm^2`