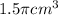1 Answer

Jim Keener · Answer 1 · 2023-10-30T12:54:18+0000

At first, we will find the volume of the cone and the volume of the sphere, then subtract them to find the answer

The rule of the volume of the cone is

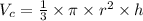
$V_c=(1)/(3)*\pi* r^2* h$

Since the height of the cone is 1 cm and its radius is 3 cm, then

h = 1 and r = 3

Substitute them in the rule above

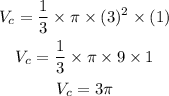
$\begin{gathered} V_c=(1)/(3)*\pi*(3)^2*(1) \\ V_c=(1)/(3)*\pi*9*1 \\ V_c=3\pi \end{gathered}$

The formula of the volume of the sphere is

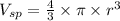
$V_(sp)=(4)/(3)*\pi* r^3$

Since the diameter of the sphere is 3 cm, then

$\begin{gathered} r=(1)/(2)*3 \\ r=(3)/(2) \\ r=1.5\operatorname{cm} \end{gathered}$

Substitute it in the formula above

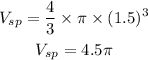
$\begin{gathered} V_(sp)=(4)/(3)*\pi*(1.5)^3 \\ V_(sp)=4.5\pi \end{gathered}$

Noe subtract them to find the answer

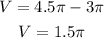
$\begin{gathered} V=4.5\pi-3\pi \\ V=1.5\pi \end{gathered}$

The amount of the extra soap is

$1.5\pi cm^3$

Please log in or register to add a comment.