Question

What is the volume of the following rectangular prism?3 1/31 2/5

Answer 1

The volume (V) of the given prism will be equal to the area of the green zone times the lenght of 1 2/5 units, that is,

`\begin{gathered} V=\text{ gre}en\text{ zone area }*\text{ lenght} \\ V=3(1)/(3)*1(2)/(5)units^3 \end{gathered}`

In order to make the product of the mixed fractions, we need to convert them into simple fraction form, that is,

`\begin{gathered} 3(1)/(3)=(3*3+1)/(3)=(10)/(3) \\ 1(2)/(5)=(5*1+2)/(5)=(7)/(5) \end{gathered}`

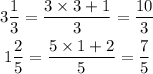
Then, the volume is given as

`\begin{gathered} V=(10)/(3)*(7)/(5) \\ V=(10*7)/(3*5) \\ V=(70)/(15) \\ V=(14)/(3) \end{gathered}`

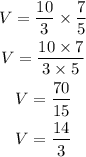
Then, the volume expressed in simple fraction form is:

`V=(14)/(3)\text{ cubic u nits}`

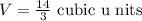
In order to convert this result into mixed form, we need to find the following division:

Then, the answer in mixed form is:

`V=4(2)/(5)\text{ cubic units}`