Question

According to a recent​ poll, 25​% of adults in a certain area have high levels of cholesterol. They report that such elevated levels​ "could be financially devastating to the regions healthcare​ system" and are a major concern to health insurance providers. According to recent​ studies, cholesterol levels in healthy adults from the area average about 260 mg/dL, with a standard deviation of about 35 mg/dL, and are roughly Normally distributed. Assume that the standard deviation of the recent studies is accurate enough to be used as the population standard deviation. If the cholesterol levels of a sample of 49 healthy adults from the region is​ taken answer parts (a) through (d). A) What is the probability that the mean cholesterol level of the sample will be no more than 210? B) What is the probability that the mean cholesterol level of the sample will be between 205 and 215? C) What is the probability that the mean cholesterol level of the sample will be less than 200?D) What is the probability that the mean cholesterol level of the sample will be greater than 222?

Answer 1

The answer is below

Explanation:

The z score is used to determine by how many standard deviations the raw score is above or below the mean. The z score is given by:

`z=(x-\mu)/(\sigma) \\\\for\ a \ sample(n):\\\\z=(x-\mu)/(\sigma/√(n) )\\\\where\ x=raw\ score,\mu=mean, \sigma=standard deviation`

Given that n = 49, μ = 260 mg/dL, σ = 35 mg/dL

a) For x < 210:

`z=(x-\mu)/(\sigma/√(n) ) =(210-260)/(35/√(49) ) =-10`

From the normal distribution table, P(x < 210) = P(z < -10) = 0.0001

b) For x > 205:

`z=(x-\mu)/(\sigma/√(n) ) =(205-260)/(35/√(49) ) =-11`

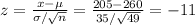
For x < 215:

`z=(x-\mu)/(\sigma/√(n) ) =(215-260)/(35/√(49) ) =-9`

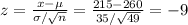
P(205 < x < 215) = P(-11 < z < -9) = P(z < -9) - P(z < -11) = 0.0001 - 0.00001 = 0.00009

c) For x < 200:

`z=(x-\mu)/(\sigma/√(n) ) =(200-260)/(35/√(49) ) =-12`

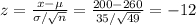
From the normal distribution table, P(x < 200) = P(z < -12) = 0.00001

d) For x > 222:

`z=(x-\mu)/(\sigma/√(n) ) =(222-260)/(35/√(49) ) =-7.6`

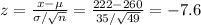
From the normal distribution table, P(x > 200) = 1 - P(z < -12) = 1 - 0.0001 = 0.9999