Question

What is the center and radius of the circle with the given equation x^2 + y^2 + 14x - 12y +69 = 0

Answer 1

Center is (7,-6)

Our radius is 4

Explanation:

Subtract 69 to both sides

Complete the square of the x terms and y terms.

`{x}^(2) + 14x`

`{y}^(2) - 12y`

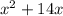
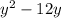
(To complete the square divide the coefficient by 2 and square it).

`((14)/(2) ) {}^(2) = 49`

`( ( - 12)/(2) ) {}^(2) = 36`

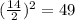
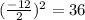
Add those terms to the full equation. Add 36 and 49 to the right side as well

`{x}^(2) + 14x + 49 + {y}^(2) - 12y + 36 = 16`

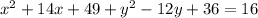
Simplify the x and y terms into a binomial.

`(x + 7) {}^(2) + (y - 6) {}^(2) = 16`

Set the left side equal to zero separately to find the center and take the square root of the right side to find the radius.

`x + 7 = 0`

`x = - 7`

`y - 6 = 0`

`y = 6`

`16 = {x}^(2)`

`4 = x`

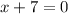
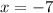
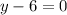
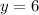
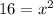
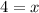
So our center is (-7,6)

Our radius is 4.