Question

Find an equation for the line below.A(5,1) B(-4,5)

Answer 1

The equation of a line has always the form

`y=m\cdot x+b`

where "m" is called its slope, and "b" is called its y-intercept. It's a well-known fact that m can be calculated using two points of the line. Let's use A and B:

`m=(-5-1)/(-4-(5))=(-6)/(-9)=(6)/(9)=(2)/(3)`

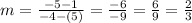
Then, our equation becomes

`y=(2)/(3)x+b`

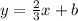
Replacing A there, we get

`\begin{gathered} 1=(2)/(3)(5)+b\Rightarrow1=(10)/(3)+b\Rightarrow\ldots \\ \ldots b=1-(10)/(3)=-(7)/(3) \end{gathered}`

Having found m and b, the final answer is

`y=(2)/(3)x-(7)/(3)`