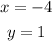We have the following system of equations:
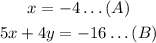
Solving by substitution method.
If we substitute equation A into equation B, we get
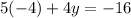
since 5(-4)= -20, we have
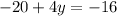
If we move -20 to the right hand side as +20, we obtain
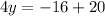
since -16+20=20-16 = 4, we get
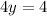
and finally, y is equal to
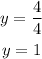
Since equation A tells us that x=-4, the solution of the system is