The exponential function is of the form:

Given the two points, we can plug each point into the equation and see:
1.
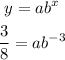
2.
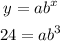
Let's divide the the 2nd equation by the 1st one:
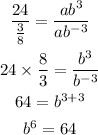
Note: we used the property of exponents, 1/a^x = a^ -x to simplify it.
Now, we can solve for b:
![\begin{gathered} b^6=64 \\ b=\sqrt[6]{64} \\ b=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jejxwa1xpr3h9rdouiu598kgsi0d8yzukv.png)
The second equation, now, becomes:
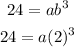
Now, we can easily find a:

We know b = 2 and a = 3.
So, the final equation will be:
