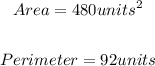Question

Can I Plss get some help on this (Number 50)

Answer 1

Step-by-step explanation:

Given;

We are given a rectangle with sides as indicated.

Required;

We are required to find the area and the perimeter from the dimensions provided.

Step-by-step solution;

We shall begin by reconstructing the rectangle and show the missing sides. This is done below;

Take note that we can extract one of the triangles and use the dimensions to calculate the missing side. This is also shown below;

Observe that we now have a triangle with sides 17 units and 16 units.

We draw a perpendicular and we effectively split the triangle into two right angled triangles. We can now solve for the side x using the Pythagoras' theorem.

`\begin{gathered} c^2=a^2+b^2 \\ Where: \\ c=hypotenuse \\ a,b=other\text{ }sides \end{gathered}`

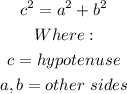
We substitute these into the formula above;

`\begin{gathered} 17^2=x^2+8^2 \\ \\ 289=x^2+64 \end{gathered}`

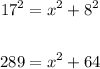
Subtract 64 from both sides;

`225=x^2`

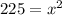
Take the square root of both sides;

`\begin{gathered} √(225)=√(x^2) \\ \\ 15=x \end{gathered}`

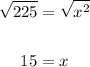
Let us now reconstruct the quadrilateral with the new dimension calculated.

We now have the Length and Width of the rectangle and we can now calculate the area and perimeter.

`\begin{gathered} AREA\text{ }OFA\text{ }RECTANGLE: \\ Area=l* w \\ \\ Area=30*16 \\ \\ Area=480 \end{gathered}`
`\begin{gathered} PERIMETER: \\ Perimeter=2(l+w) \\ \\ Perimeter=2(30+16) \\ \\ Perimeter=2(46) \\ \\ Perimeter=92 \end{gathered}`

Therefore,

ANSWER:

`\begin{gathered} Area=480units^2 \\ \\ Perimeter=92units \end{gathered}`