Question

The diameter of a circle is 20 kilometers. What is the angle measure of an arc bounding a sector with area 10pi square kilometers?Give the exact answer in simplest form. ____°. (pi, fraction,)

Answer 1

The area of a circular sector is given by:

`A=(1)/(4)\cdot\pi\cdot d^2\cdot(\theta)/(360)`

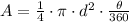
Where:

π ≈ 3.14159

d = diameter of the circle

θ = angle of the circular sector

In our problem we have that:

And we need to find the value of the angle θ. So in order to solve the problem, we replace the given data in the formula of above:

And now we solve for θ:

`\begin{gathered} 10\cdot\pi\cdot km^2=(1)/(4)\cdot\pi\cdot400\cdot km^2\cdot(\theta)/(360^(\circ)) \\ 10=100\cdot(\theta)/(360^(\circ)) \\ 360^(\circ)\cdot(10)/(100)=\theta \\ \theta=36^(\circ) \end{gathered}`

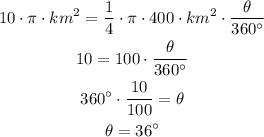
So the answer is that the angle of the circular sector is: 36°