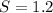Question

S varies inversely as G. If S is 4 when G is 1.8, find S when G is 6.

Answer 1

Given that "S" varies inversely as "G", it is an Inverse Variation Relationship. Then, it has this form:

`S=(k)/(G)`

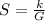
Where "k" is the Constant of Variation.

Knowing that:

`S=4`

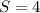
When:

`G=1.8`

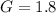
You can substitute values and solve for "k":

`\begin{gathered} 4=(k)/(1.8) \\ \\ (4)(1.8)=k \\ \\ k=7.2 \end{gathered}`

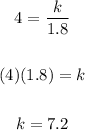
Then, the equation that models the situation is:

`S=(7.2)/(G)`

Substituting this value of "G" into the equation and evaluating:

`G=6`

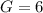
You get:

`S=(7.2)/(6)=1.2`

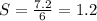
Hence, the answer is:

`S=1.2`