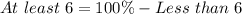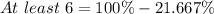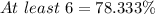Question

Temperature transducers of a certain type are shipped in batches of 50. A sample of 60 batches was selected, and the number of transducers in each batch not conforming to design specifications was determined, resulting in the following data: 1 1 2 3 0 1 3 2 0 5 3 3 1 3 2 4 7 0 2 3 0 4 2 1 3 1 1 3 4 1 2 3 2 2 8 4 5 1 3 1 5 0 2 3 2 1 0 6 4 2 1 6 0 3 3 3 7 1 2 2a) Determine frequencies and relative frequencies for the observed values of x = number of nonconforming transducers in a batch. (Enter relative frequencies to three decimal places.)x Frequency Relati veFrequency01245678(b) What proportion of batches in the sample have at most six nonconforming transducers? (Enter your answer to three decimal places.)What proportion have fewer than six? (Enter your answer to three decimal places.)What proportion have at least six nonconforming units? (Enter your answer to three decimal places.)

Answer 1

(a) See attachment for table

(b)
`Atmost\ 6 = 21.667\%`

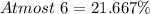
(c)
`Less\ than\ 6 = 21.667\%`

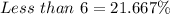
(d)
`At\ least\ 6 = 78.333\%`

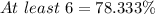
Explanation:

Given

The data (in the question)

Solving (a): Frequency and Relative frequencies of each data

The range of the data is 0 to 8. So the frequency of each is the number of times each of 0 - 8 occurs.

This is tabulated below:

`\begin{array}{ccc}x & {Frequency} & {Relative\ Frequency} & {0} & {7} & {11.667\%} &{1}& {13} & {21.667\%} & {2} & {13} & {21.667\%} & {3} & {14} &{23.333\%} & {4} & {5} & {8.333\%} & {5} &{3} &{5.000\%} &{6} &{2} & {3.333\%} & {7} & {2} & {3.333\%} & {8} & {1} & {1.667\%} \ \end{array}`

`Total\ \ \ 60`

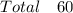
The relative frequency is calculated as:

`Relative\ Frequency = (Frequency)/(Total\ Frequency) * 100\%`

For instance: When x = 0:

`Relative\ Frequency = (7)/(60) * 100\%`

`Relative\ Frequency = (700)/(60) * \%`

`Relative\ Frequency = 11.667 \%`

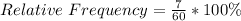
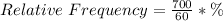
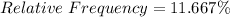
Solving (b): Proportion that have at most 6.

Here, we consider frequencies of 0 to 6.

This is represented as thus:

`\begin{array}{ccc}x & {Frequency} & {Relative\ Frequency} & {4} & {5} & {8.333\%} & {5} &{3} &{5.000\%} &{6} &{2} & {3.333\%} & {7} & {2} & {3.333\%} & {8} & {1} & {1.667\%} \ \end{array}`

Add up the relative frequencies to get the proportion

`Atmost\ 6 = 8.333\% + 5.000\% + 3.333\% + 3.333\% + 1.667\%`

`Atmost\ 6 = 21.667\%`

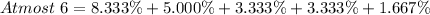
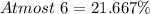
Solving (c): Proportion that have at fewer than 6.

Here, we consider frequencies of 0 to 5.

This is represented as thus:

`\begin{array}{ccc}x & {Frequency} & {Relative\ Frequency} & {4} & {5} & {8.333\%} & {5} &{3} &{5.000\%} &{6} &{2} & {3.333\%} & {7} & {2} & {3.333\%} & {8} & {1} & {1.667\%} \ \end{array}`

Add up the relative frequencies to get the proportion

`Less\ than\ 6 = 8.333\% + 5.000\% + 3.333\% + 3.333\% + 1.667\%`

`Less\ than\ 6 = 21.667\%`

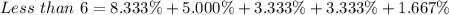
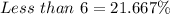
Solving (d): Proportion that have at least 6.

Here, we make use of the complement rule:

`At\ least\ 6 = 100\% - Less\ than\ 6`

`At\ least\ 6 = 100\% - 21.667\%`

`At\ least\ 6 = 78.333\%`