Question

What does the lower scale read? Answer in units of N

Answer 1

We will have the following:

First, we are given:

*Mass of the breaker: 1.1kg

*Mass of water: 3.3 kg

*Mass of metallic alloy: 4.2kg

*Density of the alloy: 5300kg/m^3

*Density of water: 1000kg/m^3

Now, we find the volume of water displaced by the alloy:

Then, from the reading in the hanging scale we will have the force experienced by the alloy due to the upthrust when placed in water, that is:

`R=mg-\rho Vg`

So:

`\Rightarrow R=33.39396226\ldots N\Rightarrow R\approx33.4N`

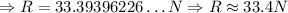
The reading on the lower scale is due to the weight of the water in the breaker and upthrust on the scale:

`R=g(m_1+m_2)+\rho Vg`

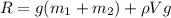
Finally:

`\Rightarrow R=50.886003774\ldots N\Rightarrow R\approx50.9N`

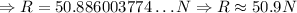
So, the readin on the lower scale is approximately 50.9N.