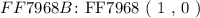We have three points that lie on a line namely, A M B, in a cartesian coordinate system.
The coordinates of each point are as such:
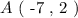
The mid-point of a line segment ( AB ) is given by coordinate ( M ) as follows:
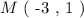
We will define the coordinates of point ( B ) in terms of cartesian coordinates as follows:
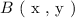
Here the line ( A B ) with points [ A, M , B ] are colinear. This means they all lie on the same line passing through all three points.
A straight line always have a constant slope/gradient ( m ) . This slope is determined between two points that lie on the line.
The formulation of calculating the slope ( m ) of the line in a cartesian coordinate system is as follows:
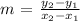
The respective cartesian coordinates of each of the two points are represented by sub-scripts of ( x and y ).
Here we will take two points ( A and M ) to determine the slope ( m ) of the line passing throgh all three points as follows:
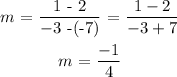
This slope ( m ) holds true for the entire line and must satisfy all consecutive points that lie on the line.
We will now consider points ( A and B ) and determine the slope ( m ):
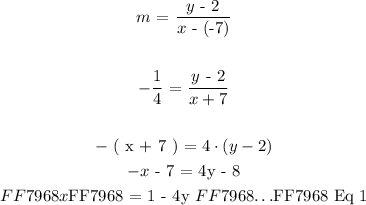
What we did above was calculated the slope ( m ) between two points ( A and B ) which resulted in an expression in terms of coordinates of point B ( x and y ). We equated that expression with the value of slope ( m ) that holds true for all points that lie on the line.
Then we used the slope equation and expressed the x-coordinate of point B in terms of y-coordinate of point B. This relaitonship is termed as Equation 1 ( Eq 1 ).
Next, we were also given that point M is the midpoint of line segment ( AB ). Using the definition of a mid-point ( M ) i.e the magnitude of line segments are:
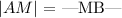
The magnitudes of line segment AM and MB must be equal for point ( M ) to be a mid-point of line segment ( AB ).
We will express the formulation of determining a magnitude of line segment using two points:
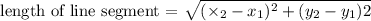
So for equating the lengths (magnitudes) of line segments ( AM ) and ( MB ) we have:
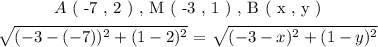
Square both sides of the equation:
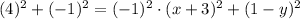
Evaluate left hand side of equation and apply PEMDAS at right hnd side of the equation:

We have two equations with two unknows ( x and y ) as follows:
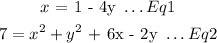
We will solve the two equation by simultaneous substitution method. Substitute Eq1 into Eq2 as follows:
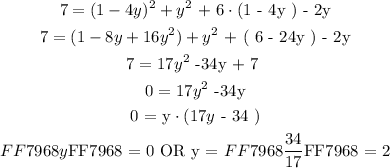
We will now plug the two values of coordinate ( y ) into ( Eq 1 ) and solve for ( x ):
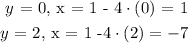
We have two solutions for the coordinates of point ( B ) as follows:
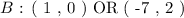
However, point B must have only one pair of coordinate. So we have to investigate both solutions given above and reject a redundant solution.
We see that solution B: ( -7 , 2 ) is redundant solution, hence, rejected. This is because it represents the coordinates of point A: ( -7 , 2 ) - given in question. So two different points can not attain the same set of coordinates! Hence,
The solution to the set of coordinates of point B is: