Question

Solve 0.9x+5.1x-7=2(2.5x-3)how many solutions does the equation have

Answer 1

We want to solve the following equation for x:

`0.9x+5.1x+7=2(2.5x-3)`

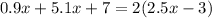
First, let's expand the parenthesis on the right side of the equation using the distributive property

`\begin{gathered} 0.9x+5.1x+7=2(2.5x-3) \\ 0.9x+5.1x+7=2\cdot2.5x-2\cdot3 \\ 0.9x+5.1x+7=5x-6 \end{gathered}`

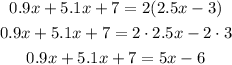
To add the terms with x, we just need to add their coefficients.

`\begin{gathered} 0.9x+5.1x+7=5x-6 \\ (0.9+5.1)x+7=5x-6 \\ 6x+7=5x-6 \end{gathered}`

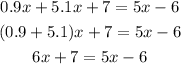
Subtracting 5x from both sides of the equation:

`\begin{gathered} 6x+7-5x=5x-6-5x \\ (6-5)x+7=(5-5)x-6 \\ x+7=0\cdot x-6 \\ x+7=-6 \end{gathered}`

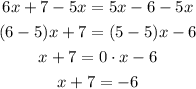
Now, if we subtract 7 from both sides, we have

`\begin{gathered} x+7-7=-6-7 \\ x=-13 \end{gathered}`

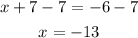
Since this is a first degree polynomial, it has only one solution and this solution is x = - 13.