To determine the probability of an event to occur, the formula is:
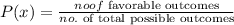
In the spinner, there are 6 possible outcomes. The arrow can either point from 1 to 6.
4.1. In the spinner, there are 3 prime numbers. These are 2, 3, and 5. Hence, there are 3 favorable outcomes if we want to have a prime number as a result after the spin. The probability of that happening will be:
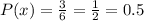
The probability of spinning a prime number is 1/2 or 0.5 or 50%.
4.2. We have already mentioned that there are 3 prime numbers (2, 3, 5). For odd numbers, we also have 3 and these are 1, 3, and 5. Combining the two, we get {1, 2, 3, 5} as either prime or odd numbers. As we can see, there are 4 favorable outcomes. Therefore, the probability is:
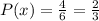
The probability of spinning a prime number or an odd number is 2/3.
4.3. We have already mentioned that there are 3 prime numbers (2, 3, 5). For multiple of 3, we only have {3, 6}. Since the given operation is AND, that means, we have to find the intersection or what's common of both data. As we can see, only {3} is common. This means, only 3 is both a prime number and a multiple of 3. There is only 1 favorable outcome. The probability is:

The probability of spinning a prime number and a multiple of 3 is 1/6.
4.4. If it has been already given that the number lands on a prime number, this means that we only have 3 choices or 3 possible outcomes. It's either 2, 3, or 5. Out of the 3 prime numbers, there are only 2 odd numbers and these are 3 and 5. Hence, the probability is:
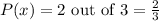
Given that a spinner lands on a prime number, the probability of spinning an odd number is 2/3.