Hello!
We have the expression:
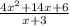
Note that all numbers in the numerator are even. So, we can put 2 in evidence, look:
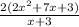
Now, let's rewrite 7x as 6x+x:
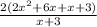
The first and second terms are multiples of 2x, so let's rewrite it putting it in evidence too:
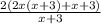
Another term appears twice: (x+3). So, we'll have:
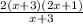
Canceling the common factors:
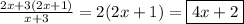
Answer:
4x +2.