Given:
The initial distance between the earth and the satellite, R₁=3.60×10⁷ m
The initial force between the earth and the satellite, F₁=400 N
The changed distance between the earth and the satellite R₂=1.80×10⁷ m
To find:
The changed force between the earth and the satellite.
Step-by-step explanation:
From Newton's gravitational law, the gravitational force between two objects is directly proportional to the product of the mass of the objects and inversely proportional to the square of the distance between them.
Let us assume that the mass of the earth is M and the mass of the satellite is m.
Thus,
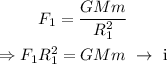
And, the changed force is given by,
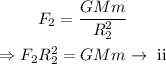
From equation (i) and equation (ii),
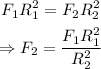
On substituting the known values,
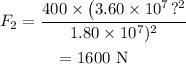
Final answer:
The magnitude of the gravitational force of attraction between the earth and the satellite after the distance between them was changed is 1600 N.