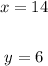Question

I need help seeing how this works out because what I am doing is not right

Answer 1

We will have the following:

AB and CD related in terms of x and y will be:

`\begin{gathered} AB=CD\Rightarrow x+y=2x-y-2 \\ \\ \Rightarrow2y=x-2\Rightarrow y=(x)/(2)-1 \end{gathered}`

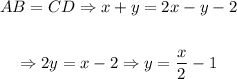
So, the equation that relates AB and CD is:

`y=(x)/(2)-1`

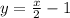
BC and DA in terms of x and y is:

`\begin{gathered} BC=DA\Rightarrow x+2y=3x-3y+2 \\ \\ \Rightarrow5y=2x+2\Rightarrow y=(2)/(5)x+(2)/(5) \end{gathered}`

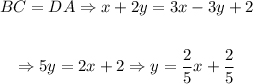
So, the equation that relates BC and DA is:

`y=(2)/(5)x+(2)/(5)`

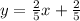
Now; we determine the values of x & y as follows:

`\begin{gathered} (x)/(2)-1=(2)/(5)x+(2)/(5)\Rightarrow(1)/(10)x=(7)/(5) \\ \\ \Rightarrow x=14 \end{gathered}`

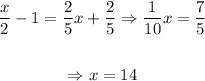
Then:

`y=((14))/(2)-1\Rightarrow y=6`

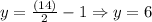
So, the values are:

`\begin{gathered} x=14 \\ \\ y=6 \end{gathered}`