Question

What is the equation of the line graphed below?A. y = -2xB. y = 2xC. y - xD. y = -x(1,2)

Answer 1

B) y = 2x

Step-by-step explanation:

We were given the following details:

The straight line passes through the origin; it passes through the point (0, 0)

The straight line passes through the point (1, 2)

`\begin{gathered} (x_1,y_1)=(0,0) \\ (x_2,y_2)=(1,2) \end{gathered}`

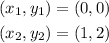
The general equation of a straight line is given by:

`\begin{gathered} y=mx+b \\ where: \\ m=slope \\ b=y-intercept \end{gathered}`

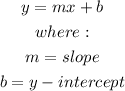
We will obtain the equation of the straight line as shown below:

I. Obtain the slope of the straight line

`\begin{gathered} \begin{equation*} slope,m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1) \end{equation*} \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(2-0)/(1-0) \\ m=(2)/(1)=2 \\ m=2 \\ \\ \therefore slope,m=2 \end{gathered}`

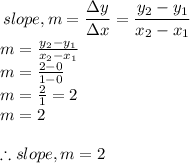
The slope of the straight line is 2

II. Obtain the y-intercept

Method 1:

The y-intercept refers to the point where the straight line crosses the y-axis.

In this case, the straight line crosses the y-axis at the origin (0, 0). This implies that:

`\begin{gathered} b=0 \\ Remember:y=mx+b \\ \Rightarrow y=2x+0 \\ y=2x \end{gathered}`

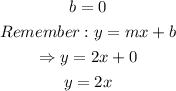
Method 2:

Using the point-slope equation:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-0=2(x-0) \\ y-0=2x-0 \\ y=2x \\ \\ \therefore y=2x \end{gathered}`

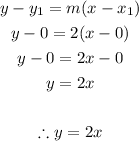
Therefore, the answer is B (y = 2x)