Question

Graph the parabola.y=1/4x^2-1Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the graph-a-function button

Answer 1

This is basic parabola of the form:

`y=ax^2-b`

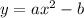
So, this one is shifted 1 units down.

The vertex is at (0, -1).

To take 2 points to the left of vertex, we find coordinates for x = -2 and x = -4.

To take 2 points to the right of vertex, we find coordinates for x = 2 and x = 4.

Let's find it:

`\begin{gathered} \text{When x = -2,} \\ y=(1)/(4)x^2-1 \\ y=(1)/(4)(-2)^2^{}-1 \\ y=0 \\ When\text{ x = -4,} \\ y=(1)/(4)x^2-1 \\ y=(1)/(4)(-4)^2-1 \\ y=3 \\ \text{When x = 2,} \\ y=(1)/(4)x^2-1 \\ y=(1)/(4)(2)^2-1 \\ y=0 \\ \text{When x= 4,} \\ y=(1)/(4)x^2-1 \\ y=(1)/(4)(4)^2-1 \\ y=3 \end{gathered}`

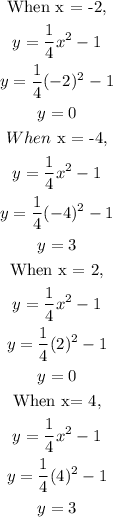
So, the 4 coordinates are:

(-2,0), (-4,3), (2,0), (4,3)

The graph: