Bisects: to divide into two equal parts.
In this case, DB is bisecting the ∠ABC, then the ∠ABD
As OP is bisecting ∠MON, that means that ∠NOP and ∠POM have the same measure.
Then:

As ∠NOP = ∠POM, we get:
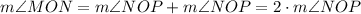
Replacing the value we get:
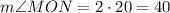
Based on this, we can use the trigonometric functions, as we have an angle and one side. Specifically, the tangent function:

First, to calculate NP, we get the following:
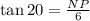
Isolating for NP:
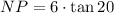
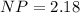
Then, calculating for MN we get the following:
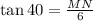
Isolating for MN:
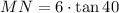
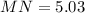
Answer:
• NP = 2.18
,
• MN = 5.03