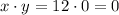We have two numbers x and y such that their difference is 12:
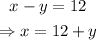
Now, we take the product of them:
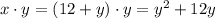
The smallest result we can get is 0 (ignoring the negative numbers, because the meaning of "small" implies an absolute value). Looking at the expression above, it is 0 for y = 0. If y = 0 then x = 12, and the difference is:
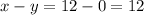
And their product is: