Question

2 groups of students group a and group B have the age distributions shown below which statement about the distributions is true

Answer 1

The ages of the students of groups A and B are displayed in the histograms.

For group A

We can determine the number of students per age by looking at the bars of the histogram

2 are 15 years old

5 are 16 years old

6 are 17 years old

5 are 18 years old

2 are 19 years old

The total students for group A is

`\begin{gathered} n_A=2+5+6+5+2 \\ n_A=20 \end{gathered}`

To calculate the average age on group a you have to use the following formula

`X^{\text{bar}}=(\Sigma x_if_i)/(n)`

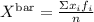
Σxifi indicates the sum of each value of age multiplied by its observed frequency

n is the total number of students of the group

For group A the average value is

`\begin{gathered} X^{\text{bar}}_A=((15\cdot2)+(16\cdot5)+(17\cdot6)+(18\cdot5)+(19\cdot2))/(20) \\ X^{\text{bar}}_A=(340)/(20) \\ X^{\text{bar}}_A=17 \end{gathered}`

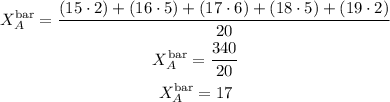
The average year of group A is 17 years old.

To determine the Median of the group, you have to calculate its position first.

`\begin{gathered} \text{PosMe}=(n)/(2) \\ \text{PosMe}=(20)/(2) \\ \text{PosMe}=10 \end{gathered}`

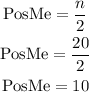
The Median is in the tenth position. To determine the age it corresponds you have to look at the accumulated observed frequencies:

F(15)=2

F(16)=2+5=7

F(17)=7+6=13→ The 10nth observation corresponds to a 17 year old student

F(18)=13+5=18

F(19)=18+2=20

The median of group A is 17 years old.

For group B

As before we can determine the number of students per age by looking at the bars of the histogram

2 are 15 years old

3 are 16 years old

4 are 17 years old

5 are 18 years old

6 are 19 years old

The total number of students for group B is

`\begin{gathered} n_B=2+3+4+5+6 \\ n_B=20 \end{gathered}`

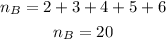
The average age of group B can be calculated as

`\begin{gathered} X^{\text{bar}}_B=(\Sigma x_if_i)/(n) \\ X^{\text{bar}}_B=((2\cdot15)+(3\cdot16)+(4\cdot17)+(5\cdot18)+(6\cdot19))/(20) \\ X^{\text{bar}}_B=(350)/(20) \\ X^{\text{bar}}_B=17.5 \end{gathered}`

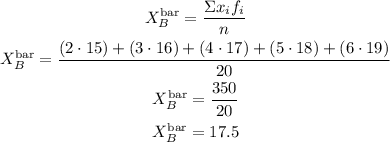
The average age for group B is 17.5 years old

Same as before, to determine the median you have to calculate its position in the sample and then locate it:

`\begin{gathered} \text{PosMe}=(n)/(2) \\ \text{PosMe}=(20)/(2) \\ \text{PosMe}=10 \end{gathered}`

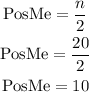
The median is in the 10nth position, to determine where the 10nth student is located you have to take a look at the accumulated frequencies:

F(15)=2

F(16)=2+3=5

F(17)=5+4=9

F(18)=9+5=14 →The 10nth observation corresponds to a 18 year old student

F(19)=14+6=20

The median of group B is 18 years old

So

`\begin{gathered} X^{\text{bar}}_A=17 \\ X^{\text{bar}}_B=17.5_{} \\ Me_A=17 \\ Me_B=18_{} \end{gathered}`

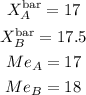
The mean and median of group B are greater than the mean and median from group B. The correct choice is the first one.