Given the system of equations:
3x + 3y = 18
2x + y = 4
Let's solve the system of equations using the elimination method.
Multiply one equation by a number which makes one variable of each equation opposite.
Multiply equation 2 by -3:
3x + 3y = 18
-3(2x + y) = -3(4)
3x + 3y = 18
-6x - 3y = -12
Add both equations:
3x + 3y = 18
+ -6x - 3y = -12
_________________
-3x = 6
Divide both sides by -3:
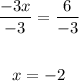
Substitute -2 for x in either of the equations.
Take the second equation:
2x + y = 4
2(-2) + y = 4
-4 + y = 4
Add 4 to both sides:
-4 + 4 + y = 4 + 4
y = 8
Therefore, we have the solutions:
x = -2, y = 8
In point form, we have the solution:
(x, y) ==> (-2, 8)
ANSWER:
(-2, 8)