SOLUTION
From f(x) = 6.4 sin(x) + 5.9 cos(x)
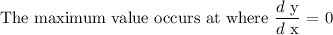
So we will differentiate the function f(x) = 6.4 sin(x) + 5.9 cos(x)
f(x) = 6.4 sin(x) + 5.9 cos(x)
f'(x) = 6.4 cos(x) - 5.9 sin(x)
6.4 cosx - 5.9 sinx = 0
Squaring both sides we have
![\begin{gathered} 6.4\cos x\text{ + 5.9sinx = 0 } \\ \text{recall that cos x = }\sqrt[]{1-sin^2x} \\ 6.4\text{ }\sqrt[]{1-sin^2x}\text{ + 5.9sinx = 0 } \\ 6.4\text{ }\sqrt[]{1-sin^2x}=\text{ -5.9sinx} \\ \text{square both sides } \\ 40.96(1-sin^2x)=34.81sin^2x \\ 40.96-40.96sin^2x\text{ = }34.81sin^2x \\ 40.96=75.77sin^2x \\ \sin ^2x\text{ = 0.541 taking squaroot} \\ \text{sinx = }\sqrt[]{0.541} \\ \sin x\text{ = 0.735} \\ x\text{ = }\sin ^(-1)0.735 \\ x\text{ = 47.35} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nz0dyuizey5rvaa84lvjrl298mxkta5f0s.png)
We have gotten the value for x, now let's find our maximum and minimum values
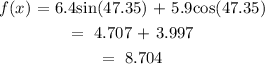
Therefore, the maximum value is 8.704 and the minimum value is -8.707
Note that maximum value is just the direct opposite of minimum value