Question

What is the equation of the graphed function?A. f(x) = -1/3x + 1B. f(x) = 3x + 1C. f(x) = 1/3x + 1D. f(x) = -3x + 1

Answer 1

Step-by-step explanation

If (x,y) is a point in the graph of a line then its coordinates x and y form a solution to the equation of that line. In slope-intercept form this equation looks like this:

`y=mx+b`

What we are going to do here is choose two points from the line in the picture and use them and the expression above to construct two equations for m and b.

As you can see (0,1) and (3,0) are part of the line so we have the following two equations:

`\begin{gathered} 1=m\cdot0+b \\ 0=3m+b \end{gathered}`

From the first equation we get b=1. If we use this value of b in the second equation we obtain the following:

`\begin{gathered} 0=3m+b=3m+1 \\ 0=3m+1 \end{gathered}`

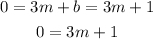
We can substract 1 from both sides:

`\begin{gathered} 0-1=3m+1-1 \\ -1=3m \end{gathered}`

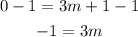
Then we divide both sides by 3:

`\begin{gathered} -(1)/(3)=(3m)/(3) \\ m=-(1)/(3) \end{gathered}`

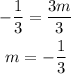
Then we have this equation for the line in the picture (we take y=f(x)):

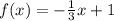
`f(x)=-(1)/(3)x+1`Answer

Then the answer is option A.