Solution
- a and b are integers. a | b means that integer a can divide integer b with no remainders.
- Let the Quotient of the division be k, so we can say:
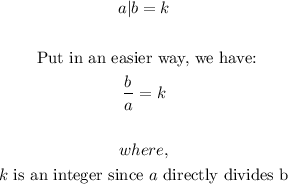
- Now, we are asked to find
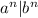
- Again, we can rewrite this as:
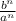
- We can rewrite this expression using the law of exponents that says:
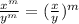
- Applying this law, we have:
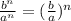
- But we already know that
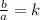
- Thus, we have that:
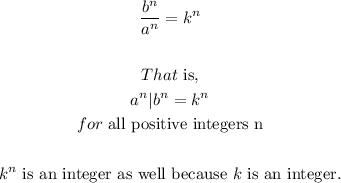
- Therefore, we have successfully proved the assertion