Question

Hi can you help me with this question real quick please

Answer 1

The volume of a sphere is given by

`V=(4)/(3)\pi r^3`

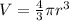
where V denotes the volume and r the radius. In our case,

`r=(3)/(2)in`

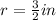
Then, by substituting this value into the formula, we have

`V=(4)/(3)\pi((3)/(2))^3`

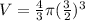
which gives

`\begin{gathered} V=(4)/(3)\pi(3^3)/(2^3) \\ V=4\pi(3^2)/(8) \\ V=\pi(9)/(2) \end{gathered}`

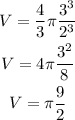
By taking Pi as 3.14, we get

`V=14.13in^3`

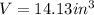
So , by rounding to the nearest tenth, the answer is 14.1 cubic inches.