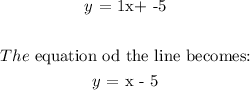Answer:
y = x - 5
Step-by-step explanation:
Given:
The points are (-1, -6) and (6, 1)
To find:
the equation of line that pass through the points
To determine the equation of the line, it will be in the form:
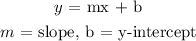
The slope formula is given as:
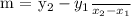
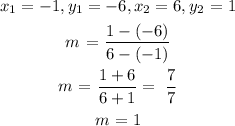
To get the y-intercept, we will use any of the given points and the slope
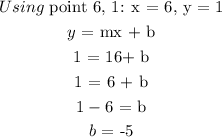
Next substitute the slope and y-intercept