Question

I could use some help on math I’m really struggling

Answer 1

We need to find how much will be left after 6 half-lives of a radioactive isotope starting with 130g.

One way to write the amount N of radioactive isotope left after a time t, with an initial amount N₀ and a half-life τ is:

`N=N_0\left((1)/(2)\right)^{t\text{ /}\tau}`

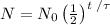
Notice that when t = τ, we have:

`N=(N_0)/(2)`

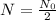
In this problem, we have:

`\begin{gathered} N_0=130g \\ \\ t=6\tau \end{gathered}`

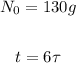
Then, we obtain:

`N=130g\left((1)/(2)\right)^{6\tau\text{ /}\tau}=130g\left((1)/(2)\right)^6=(130g)/(64)\cong2\text{ g}`

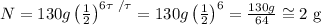
Therefore, rounding to the nearest gram, the answer is 2 grams.