Let R be the minutes Tisha runs and W be the minutes Tisha walks. Since she requires 24 minutes to do 6 laps running and 3 laps walking, we have the following equation:
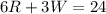
Now, when she requires 20 minutes to do 6 laps running and 2 laps walking, we have:
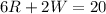
So, we have the following system of equations:

We are going to solve it by elimination. Notice that the coefficients of R are the same, so we just have to multiply one equation by -1 and add it altogether to the other equation:
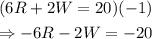
Then:
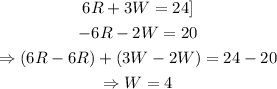
Now we use the value W=4 to find R:
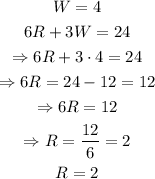
Therefore, it takes Tisha to complete a lap 2 minutes if she's running and 4 minutes if she's walking.