Here, we want to get the range and the domain of the function
The domain refers to the x-values
Looking at the plot, we can see the x-values from 2 to 6
In an interval form, we have this as;
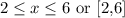
For the range values, we have these as the possible y-values
We can see that the lowest y value is at -4 and the highest y-value is at the point y = 5
So the range is;
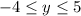
Now, we want to answer if the relation is a function
For a relation to be a function, no domain value will have 2 range values
But, we can have a single range value having two domain values
As we can see, this rule is correctly followed on the plot and thus, we can confirm that the relation is a function
It is a function because each of the x-values have a single y-value. This means that for every domain value, there is only a range value attached