Question

We want to solve the following system of equations.x^2 + y^2 = 1y = 2x + 2One of the solutions to this system is (-1,0).Find the other solution.

Answer 1

(-3/5, 4/5)

Step-by-step explanation:

Given the system of equations:

`\begin{gathered} x^2+y^2=1 \\ y=2x+2 \end{gathered}`

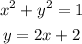
First, we substitute y=2x+2 into the first equation to obtain:

`\begin{gathered} x^2+(2x+2)^2=1 \\ x^2+(2x+2)(2x+2)=1 \\ x^2+4x^2+4x+4x+4=1 \\ 5x^2+8x+4-1=0 \\ 5x^2+8x+3=0 \end{gathered}`

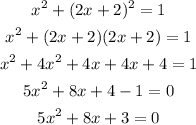
We solve the derived quadratic equation for x,

`\begin{gathered} 5x^2+8x+3=0 \\ 5x^2+5x+3x+3=0 \\ 5x(x+1)+3(x+1)=0 \\ (5x+3)(x+1)=0 \\ 5x+3=0\text{ or }x+1=0 \\ x=-(3)/(5)\text{ or -1} \end{gathered}`

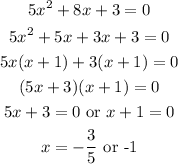
We then solve for the corresponding values of y using any of the equations.

`\begin{gathered} \text{When x=-1} \\ y=2x+2 \\ y=2(-1)+2 \\ y=0 \\ When\text{ }x=-(3)/(5) \\ y=2(-(3)/(5))+2 \\ =(4)/(5) \end{gathered}`

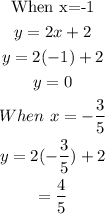
Therefore, the solutions o this system are:

(-1,0) and (-3/5, 4/5).

The other solution is (-3/5, 4/5).