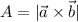The area of a paralellogram with base a and height h is given by:
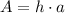
If two adjacent sides of a parallelogram have lengths a and b and are separated by an angle φ, then the base of the parallelogram is a and the height is given by b*sin(φ). Then, the area of the parallelogram is given by:

On the other hand, the cross product of two vectors is defined as:
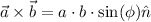
Where the unitary vector is directed toward the direction perpendicular to a and b according to the right hand rule.
The modulus of the cross product of a and b is:

We can see that both the area of the parallelogram and the modulus of the cross product have the same expressions. Therefore: