Question

Please help me work through this, thank you for your time!

Answer 1

Given

The equation of the height is

`h(t)=-16t^2+20t+950`

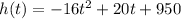
To find

The velocity when the stone reach the ground

Step-by-step explanation

When the stone reaches the ground

`\begin{gathered} h(t)=0 \\ \Rightarrow-16t^2+20t+950=0 \\ \Rightarrow16t^2-20t-950=0 \\ \Rightarrow t=(20\pm√(20^2-(4*16*(-950)))/(2*16) \\ \Rightarrow t=(20\pm247.38)/(2*16)=8.35\text{ s} \end{gathered}`

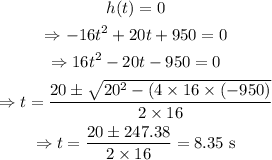
Thus the time taken to reach the ground is 8.35s . (Here only the positive value is considered)

We know the velocity is the change in distance per unit time,

Thus,

`\begin{gathered} v(t)=h^(\prime)(t) \\ \Rightarrow v(t)=-32t+20 \end{gathered}`

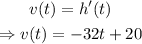
At t=8.35 s

`\begin{gathered} v(8.35)=-32*8.35+20 \\ \Rightarrow v(8.35)=-247.2\text{ feet/s} \end{gathered}`

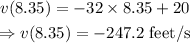
Conclusion

The velocity is -247.20 feet/s