When you flip a coin, there are only two possible outcomes, heads (H) or tail (T).
If you consider the coin to be fair, then both outcomes have the exact same probability which can be calculated as the number of favorable outcomes divided by the total number of outcomes.
For the event "flip a coin" the probability of obtaining tail is:
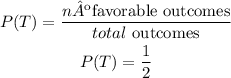
The experiment consists on flipping the coin 8 times:
The coin is flipped 8 times, so the number of trials of the experiment is fixed (n=8).
Each trial has only two possible outcomes "Head"(failure) or "Tail" (success)
The probability of the result being tail is the same for each time the coin is flipped, this represents the probability of success of the experiment (p=0.5).
Each trial of the experiment (flipping the coin) is independent.
This experiment meets the binomial criteria, which means that it is a binomial experiment.
To calculate the probability you can apply the formula for the binomial probability:
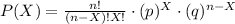
Where
n is the number of trials
X is the number of successes
p is the probability of success
q is the probability of failure and is complementary to p
For this experiment:
The number of trials is n=8
The number of successes is X=7
The probability of success is p=0.5
The probability of success is q=1-p=1-0.5=0.5
Use these values to calculate the probability of obtaining 7 tails:
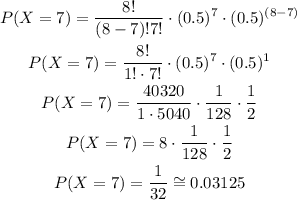
The probability of getting 7 tails when flipping the coin 8 times is
P(X=7)= 0.03125